Page 160 - Nuovo Gulliver News Marzo 2022 - Rivista

5 ª

Matematica

posta di utilizzare la piegatura della ancora una volta per far rilevare che tra circonferenza e cerchio, specifi-
carta per eseguire la consegna, pro- dopo aver effettuato la prima piega a cando che con il termine circonfe-
poniamola noi e stimoliamo la con- metà sarà possibile effettuare la se- renza si intende parlare di una linea
versazione chiedendo: conda senza la necessità che questa chiusa e con il termine cerchio della
4 Quante pieghe serviranno? divida a metà la figura piegata, purché porzione di superficie piana racchiusa
4 Come devono essere fatte? i bordi curvi coincidano. dalla circonferenza, cioè la sua re-
4 Quale relazione hanno fra loro le gione interna.
pieghe?
Lasciamo liberi i ragazzi di sperimen- Disegniamo con lo
tare: comprenderanno presto che una spago
piega non è sufficiente per poter indi- Distribuiamo a ogni alunno un car-
viduare il centro del cerchio, ma che La prima piega infatti rappresenta un tellone e chiediamo ai ragazzi come
ne sono necessarie almeno due. Non diametro del cerchio, la seconda in- procederebbero per disegnare una
tutte le pieghe effettuate, però, permet- vece ne determina due raggi. circonferenza abbastanza precisa su
tono di trovare il centro: talvolta non una grande superficie: il compasso
rappresentano altro che corde della risulterà troppo piccolo, quindi pro-
circonferenza, cioè segmenti che con- poniamo di utilizzare uno spago, una
giungono due punti qualsiasi. puntina e una matita. Raccogliamo
le loro ipotesi su come procedere e,
dopo aver consegnato loro i materiali,
Con delle semplici piegature siamo invitiamoli a sperimentare per trovare
così riusciti a far prendere confidenza una soluzione. Se non dovesse per-
con il cerchio e le sue parti princi- venire, forniamola noi: facciamo po-
pali: circonferenza, centro, diametro sizionare la puntina su un punto più
Basterà piegare il nostro cerchio a e raggio. o meno centrale del cartellone senza
metà e poi ancora a metà per trovare Sottolineiamo agli alunni la differenza fissarla ancora (sarà il centro del cer-
con sicurezza il centro: si individue-
ranno, così, due diametri del cerchio, Matematica 5 ª
cioè due segmenti che uniscono due PASSIONE PAVIMENTAZIONE scheda n. 1
punti qualsiasi della circonferenza
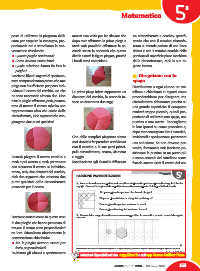
Anna vuole realizzare una pavimentazione utilizzando piastrelle quadrate e piastrelle triangolari bianche
passando per il centro. e grigie. Osserva l’immagine della superficie da tassellare e completala. Poi rispondi alle domande.

Di quante piastrelle quadrate bianche avrà bisogno? ...................................................................................................................
Di quante piastrelle bianche triangolari avrà bisogno? ...............................................................................................................

Quante piastrelle quadrate serviranno in tutto? .........................................................................................................................................
Quante piastrelle triangolari serviranno in tutto? .....................................................................................................................................
Osserva i due esagoni e realizzane un terzo sempre diviso in tre rombi e tenendo conto della regola
Facciamo notare come in questo caso nascosta.
le due pieghe che hanno permesso di
trovare il centro sono perpendicolari
tra loro. Stimoliamo ulteriormente la
conversazione chiedendo:
4 Ma le pieghe devono essere per
forza perpendicolari? COSA VERIFICARE: realizza tassellazioni del piano con figure date; rappresenta un esagono rispettando le regole esplicite e implicite.
Patrizia Damiolini © Edizioni Didattiche Gulliver S.r.l.
Invitiamo gli alunni a sperimentare
Soluzioni disponibili nel sito mygulliver.it e nell’app Nuovo Gulliver News

NUOVO NEWS n. 230 marzo 2022 159